| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- flaks
- 딥러닝
- 리멤버나우 요약
- 이베이 매각
- C++
- Convolutional Neural Networks
- 110 옮기기
- git password
- 웹 독학
- 스무고개 Metric
- 경제 요약
- but how?
- 2003 에러
- 리멤버나우
- 백준 2193
- 코딩테스트
- 2003 error
- 오픈소스
- git-lfs
- pytorch-tutorial
- multi-task learning
- 프로그래머스 여행경로
- 장영준
- cs231
- aws rds
- 뤼이드
- 프로그래머스
- 알고리즘
- flask
- 미국 이란 전쟁
- Today
- Total
Nam's
[딥러닝] cs231n-04 Backpropagation & Neural Networks Intro 본문
[딥러닝] cs231n-04 Backpropagation & Neural Networks Intro
namespace 2020. 3. 2. 00:27*본문 내용은 스탠포드 대학교 CS231n 강의를 개인적인 학습 목적으로 요약한 내용입니다.
Lecture: Introduction to Neural Networks
Slide: http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture4.pdf
1. Backpropagation
지난 3강 정리에서 Optimization을 다뤘다. 우리가 목표한 Label (정답)과 model을 통해 나온 Output이 얼마나 차이(Loss)가 나는지 Gradient를 통해 찾고, 수정하는 것을 Optimization이라고 한다.
그렇다면 구체적으로 어떻게 function node 들의 Gradient를 구할 수 있을까? 특히 Neural Networks 처럼 깊이 있는 모델에서는 어떻게 하면 효과적일까? Backpropagation(역전파)이 필요하다.
최종 output 노드에서부터 모델 뒤로 한 노드 씩 넘어가면서 각 노드의 Gradient를 구한다.
각 노드의 Gradient는 Chain Rule (연쇄법칙)을 이용해서 구할 수 있다.
Chain Rule
연쇄 법칙은 고등학교 시절 살짝 배운 적이 있는데, 두 개 이상의 함수가 결합된 합성함수를 미분할 때 필요하다.
f(x)의 도함수 (미분값)은 f'(x) 인 것을 쉽게 알 수 있지만, f(g(x))의 경우 혹은 f(g(h(k(x)))) 같은 합성함수의 경우 복잡할 수 있다. 이때, 도함수의 정의를 알아보면 chain rule을 이해할 수 있다.
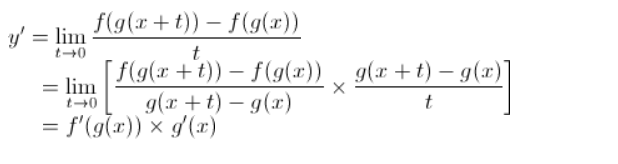
이와 같은 방식으로 복잡한 합성함수를 잘게잘게 쪼개서 곱하기, 더하기 수준으로 나타낸다.
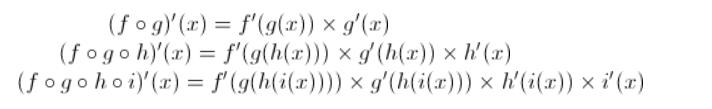
Sigmoid Function의 경우 함수가 복잡하지만 Chain Rule로 쪼개면 다음과 같이 간단해진다.
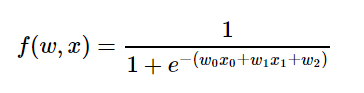
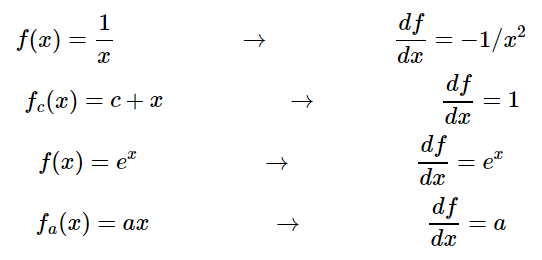
더 자세한 내용은 아래 블로그에 잘 정리되어 있다.
Chain Rule: [수학벙커] 체인룰
Sigmoid Propagation: http://aikorea.org/cs231n/optimization-2/#sigmoid
*Backpropagation의 결과로 나온 각 Gradient들은 각 노드가 최종 출력에 얼마나 특별한 영향을 미치는지를 의미한다.
Codes
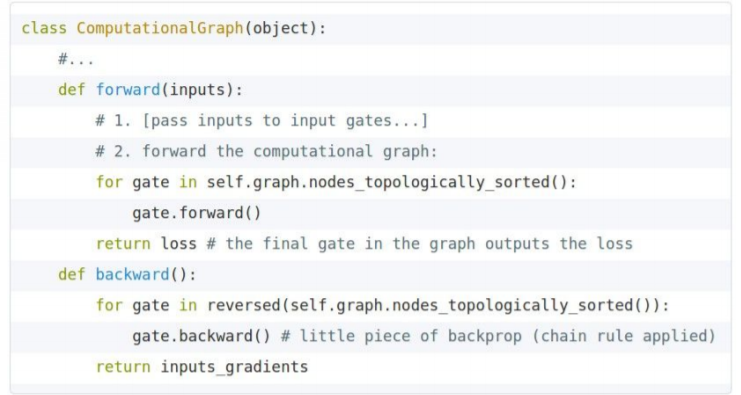
전체적인 코드는 forward pass와 backward pass로 나누는 API로 생각할 수 있겠다.
forwad pass에서는 노드의 output을 계산하는 함수를 구현하고, backward pass에서는 gradient를 계산한다.
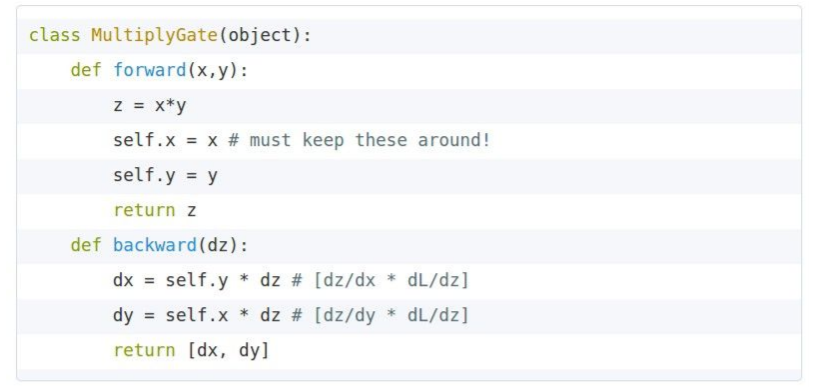
각 gate 내부를 구현할 때 중요한 것은, forward pass의 값을 저장(cache)해야 하는 것이다. 위의 코드에서도 볼 수 있듯이 backward pass 과정에서 저장된 값들을 다시 사용하기 때문이다.
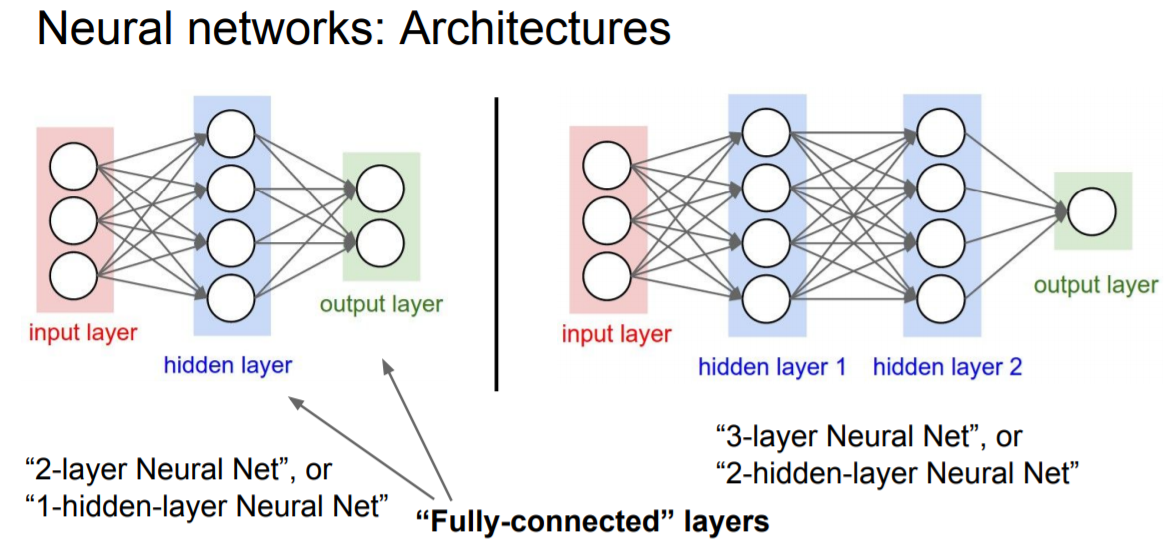
2. Neural Networks
Neural Network (신경망)은 간단하게 말하자면 Function(함수)들의 집합이다.
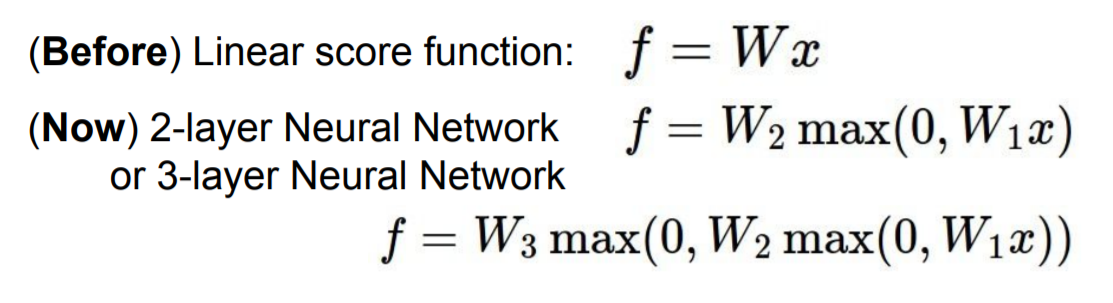
Layer가 많아지고 깊어지면 그게 Deep Neural Networks이다.
보다 자세한 내용은 앞으로 다음 강의들에서 다룰 예정이다.
다음은 앞으로 배울 내용들이다.
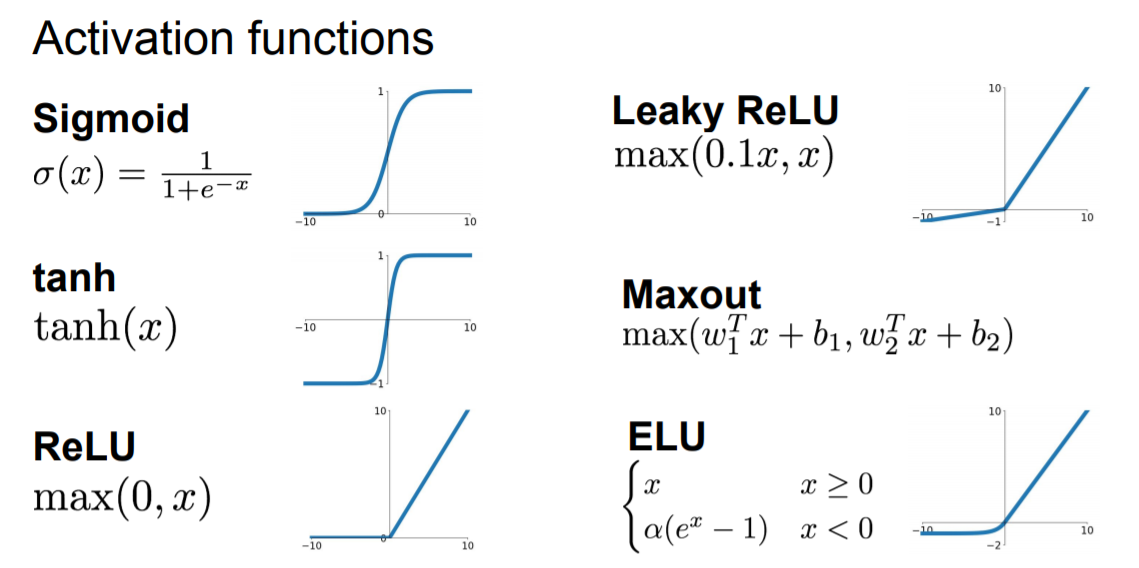
'개발 > Machine Learning' 카테고리의 다른 글
| [딥러닝] cs231n-05 Convolutional Neural Networks (0) | 2020.03.03 |
|---|---|
| [딥러닝] cs231n-03 Loss Function & Optimization (0) | 2020.02.28 |
| [딥러닝] CS231n-02 이미지 인식의 어려움, kNN, Linear Classfier (0) | 2020.02.27 |



